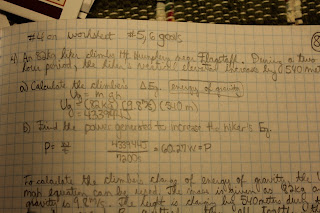Light Problem (Mirrors and Lenses)

A candle with a flame 1.5cm tall is placed 5.0cm from the front of a concave mirror.  A virtual image is produced that is 10cm from the vertex of the mirror. (a) Find the focal length and radius of curvature of the mirror (b) How tall is the image of the flame?

Energy Problem (The Hiker)

To calculate the climber's change of energy of gravity, the Ug=mgh equation can be used.  The mass is given as 82kg and gravity is 9.8m/s.  The height is changing by 540meters during the two hour period.  By multiplying them all together, the change in energy due to gravity is 433944Joules.

The second part of the question asks to find the power needed to increase the hikers Eg.  Here, the power equation can be used which is Power equals work divided by time.  The work is the change in energy just calculated, 433944Joules.  The time is 2hours which needs to be converted to seconds to be calculated properly.  One hour contains 3600seconds.  Therefore, 3600seconds multiplied by 2hours equals a time of 7200seconds.  Finally to find the power, take the work, 433944Joules, divided by the time in seconds, 7200seconds, to find the power generated which is 60.27W.  60.27W represents the power generated to increase the hiker's Eg.

Energy Problem (The Roller Coaster)

A roller coaster travels on a frictionless track as shown in Fig 5.31. (a) If the speed of the roller coaster at point A is 5.0m/s, what is its speed at point B? (b) Will it reach point C? (c) What minimum speed at point A is required for the roller coaster to reach point C?

To create the bar graphs, the knowledge of what K, Ug, and Us is in order.  While Ug represents the height of the object, K symbolizes the potential energy and Us represents a spring energy.  During point A, the initial energy graph needs an equal amount of K and Ug.  This is because the roller coaster is 5.0meters off the ground and therefore has the potential energy, Ug, to go down the hill.  There is no spring throughout this ride.  At point B, the intermediate energy the height, Ug, is gone and transferred to potential energy, K.  Since the roller coaster started out with 5.0m/s velocity and at the top of a hill, the coaster now needs all the energy it lost from its height, Ug, in potential energy to make it up the second hill.  By point C, the final energy graph represents the transfer of all the energy to Ug, height.  The coaster is now at 8.0 meters in height, which is taller than the first hill.  The potential energy it had at points A and B were used to propel the roller coaster to point C.

The speed at point B can be calculated with the equations K, potential energy, equals 1/2 mass multiplied by velocity squared and Ug, height, equals mass multiplied by gravity, 9.8m/s, and height, in meters.  Since the mass of the coaster isn't given, the combination of the equations need to be used to find the speed at point B.  If 1/2 mass times velocity squared plus mass times gravity times height is put equal to 1/2 mass times velocity at point B squared, the velocity can be determined.  Because the mass isn't given, one can begin by dividing the entire equation by mass.  Then, plug in the numbers-1/2 (5m/s) squared + (9.8m/s) (5m) equals 1/2 B's velocity squared.  B's velocity is then found to be 11.09m/s.

To find if the coaster reaches point C, the right side of the equation above is used equaled to the height equation, Ug equals gravity times height times mass.  Again, divide the entire equation by mass.  Plug in the numbers, 1/2 (5m/s) squared + (9.8m/s) (5m) equals (9.8m/s) times height.  By solving for height, the height comes out to be 6.28m.  The coaster doesn't reach point C at 8meters.

Finally to locate the minimum speed, velocity, required to reach point C from point A, use the equation from the last paragraph keeping the velocity as the variable, 1/2(v) squared + (9.8) (5m) ='s (9.8) (8).  The height of A is used in the first half of the equation because the coaster starts here and ends at 8meters.  That's why 8meters is used in the second half of the equation. The velocity needed at point A to reach 8meters at point C is 7.67m/s.

Circular Motion Problem

The centripedal force is defined as the mass times the velocity squared divided by the radius of the loop.  The mass of the person is 55kg and her velocity she is traveling by is 65m/s while the radius of the loop is 380m when plugged into the formula the force is 612N.  612N is the force that is pushing the airplane out towards the rim of the loop.

The weight or gravity force is always and can be calculated by multiplying the mass of the women by the gravity force.  The centripetal force calculated before is bigger at 612N, because the centripetal is larger antoher force is therefore normal force.  Since the weight and centripetal forces should equal each other in order to keep the rider from being thrown off the plane.  The Fn is calculated using math skills.  Fa plus Fn must equal 612N. Fo equals 539N.  Using math Fn is found to be 73N.  This 73N force is most likely provided by a protector or harness or any other mechanism keeping the person strapped in.  This is balancing the forces.  The Fn is downward along with the weight force in order to create the state of equilibrium.

The woman is pushed out with 612N when it's greater than the persons weight force pull (539N) because of its greater force exerted outwards.  The person feels lighter than usual.

The Fl represents the normal force on the human.  The Fn or W is the weight force of the human while in the air.  The Fl arrow is straight up to counteract the weight force or Fn arrow.  The two forces need to unbalance or in this case be different because the human is in motion at the time.

Momentum (Collision) Problem

First, grams needs to be converted to kg so the 15g is divided by 1000g which is one kilo.  The 15grams is then converted to 0.015kg.

To find the change in momentum, mass is multiplied by change in velocity.  The velocity is given as 600m/s and the mass was just calculated as 0.015kg.  The change in momentum is found to be 9N.m.  This is the change of the first vehicle.

Next, the other car is 100grams and should be divided by 1000grams which is one kilo to find out the car is 0.1kg in mass.

The change of velocity of both cars is next found with the equation change in momentum equals mass times change in velocity.  The change of momentum was found as 9N.m.  The two masses are added together to find the change of velocity form both cars.  Added together, the mass of 0.115kg is divided by the momentum of both cars.  Finally, the change of velocity in both cars is found as 78.26m/s.

Momentum (Impulse Problem)

The equation of change in momentum equals force multiplied by change in time is implemented.  The problem gives 1320N of net force is acting on the ball.  It also gives 9.0 times 10 to the negative third power seconds as the change in time the ball goes.  By multiplying the Force and change of time together, the momentum is calculated as 11.88N/s.

The to find the change in velocity, the equation change in momentum equals mass multiplied by change in velocity.  The momentum was found to be 11.88N/s, and earlier the mass is given as 140g.  Since the mass is needed in Kg, one will  need to divide 140g by 1000grams because that is 1 Kilo.  The mass will then equal 0.140 kg.  With the mass, one is finally able to divide the momentum of 11.88N/s by the mass, 0.140kg, to find the change in velocity which is 84.86m/s.

Contact Forces Problem

A crate resting on a floor has weight, normal, friction, and Force forces.  The normal and weight forces are balanced.  The friction and Force forces aren't balanced because the object is moving forward therefore there is a positive force to the right.  Friction is negative because it takes away force by slowing it down.

To find the weight force, mass multiplied by acceleration is enforced (ma=W).  The weight force is negative because acceleration is negative (-9.8m/s2).

Normal force and weight force are balanced, so the normal will equal the weight force except a positive number.  The normal and weight forces added together should equal zero.

Next, the frictional force should be calculated using the friction equals mu multiplied by Normal equation. N signifies normal force, while M represents the coefficient of friction.  The coefficient of friction is given (0.15) and is mulitplied by the Normal just calculated (490N) to find friction (73.5N).

Finally to calculate acceleration, the equation Net Force equals mass multiplied by acceleration should be used.  EF signifies net force which will be Force subtracted by friction.  The mass is given in the problem (50kg).  To solve for acceleration, subtract the friction force from the Force.  Then, divide that number by the mass to find acceleration.